

Retarders change the polarization state of light by introducing a phase shift between two orthogonal polarization components. The phase shift is usually specified in units of the wavelength λ. The most common values are λ/2 (to rotate a linear polarization) and λ/4 (to change linear polarization to circular and vice versa).
We offer large variety of types for retarders. The following description of some important properties of retarders is intended to provide some guidance in the choice of a suited type for a particular application.
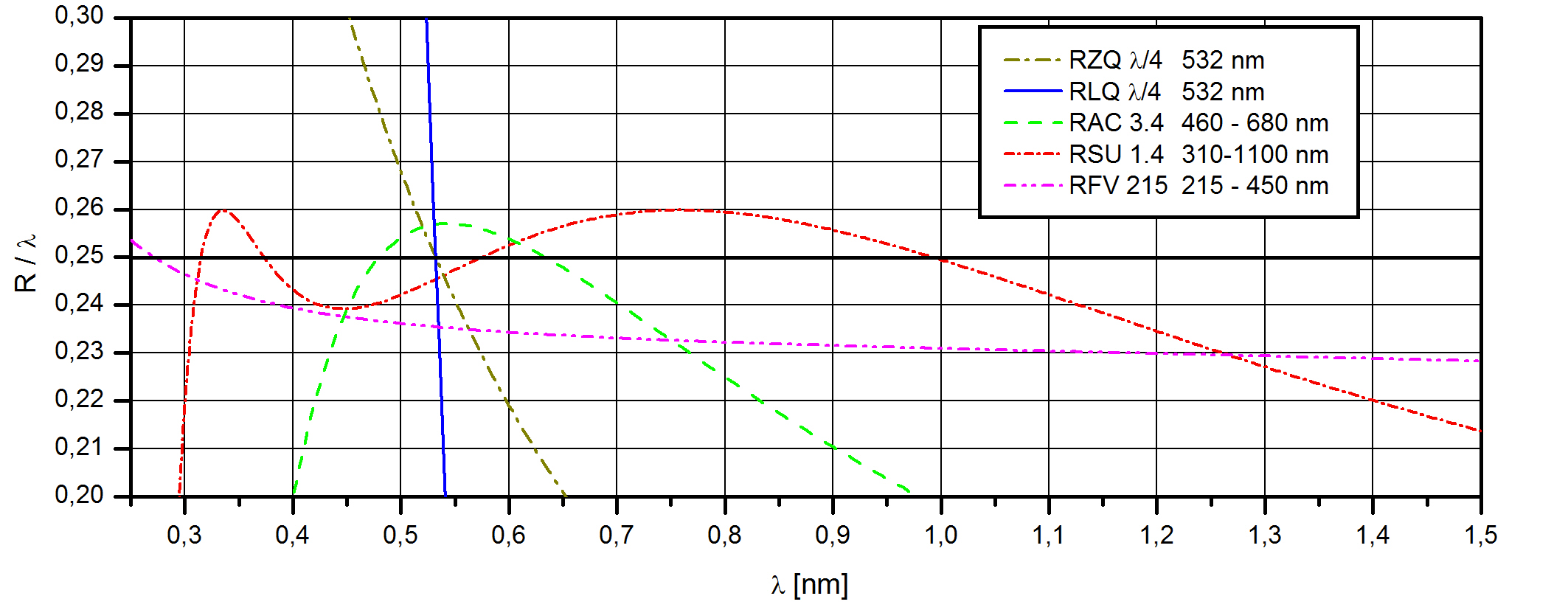
The diagram shows the spectral variation of the path difference R versus the wavelength λ for several types of retarders from our delivery program. Low order plates (RLQ) and zero orthe plates (RZQ) are optimized for a single wavelength and can be used in a narrow spectral range. For broader spectra we offer achromatic (RAC) or superachromatic retarders (RSU) which compensate the change of the phase shift by a combination of different birefringent materials. Fresnel rhombs (RFV, Fresnel-Rhombs) generate the phase shift by total internal reflection rather than by birefringence. This makes them suited for applications requiring a constant phase shift over an extremely broad spectral range.
The most common retarders (low orthe and zero orthe) are made of plates from a single material. The path difference R is determined by the plate thickness d and the material specific difference of refractive indices µ=ne-no according to R = d•µ. From the path difference one can calculate the phase shift Δ at an arbitrary wavelength λ:
As the value of R is known to be λ0/2 bzw. λ0/4 at the design wavelength this allows a good estimation of spectral variation of Δ.
The path difference changes depending on the temperature. Retarthes are usually manufactured for operation at room temperature. If the temperature change δT is not too large a linear variation of the path difference can be assumed. The temperature coefficient α is a result from the thermal expansion coefficient and the thermal coefficient of the birefringence:
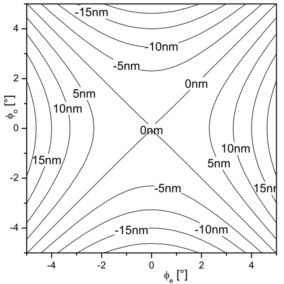
The diagram depicts the change R-R0 for a typical zero-orthe plate (β ~ 1nm/deg2 ). Most types of retarthes show a similar pattern with different values of β. A tilt around the diagonal between the principal axes leaves the path difference nearly unchanged. Superachromatic plates and Fresnel rhombs show a different behavior unthe tilt.